Distance vector routing protocols
A distance vector routing protocol in data network determines the best route for data packet based on distance. Distance vector routing protocol measure the distance by the number of routers a packet has to pass, one routers counts as one hop. Distance vector routing protocols use the Bellmen- ford algorithm and fork - fulkerson algorithm to calculate the best route. Distance vector routing protocol requires that a router inform it's neighbours of topology changes periodically. Historically known as the old ARPANATE routing algorithm known as bellmen-ford algorithm.
Distance vector routing algorithm is distributed algorithm . This routing algorithm is a iteration algorithm. Whenever a packet comes to router the neighbouring router will give the vector table and a new vector table is created at that router.
Distance Vector Routing Algorithm-
| Distance Vector Routing is a dynamic routing algorithm. |
It works in the following steps-
Step-01:
Each router prepares its routing table. By their local knowledge. each router knows about-
- All the routers present in the network
- Distance to its neighboring routers
Step-02:
- Each router exchanges its distance vector with its neighboring routers.
- Each router prepares a new routing table using the distance vectors it has obtained from its neighbors.
- This step is repeated for (n-2) times if there are n routers in the network.
- After this, routing tables converge / become stable.
Bellman Ford Basics – Each router maintains a Distance Vector table containing the distance between itself and ALL possible destination nodes. Distances,based on a chosen metric, are computed using information from the neighbors’ distance vectors.
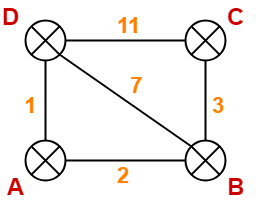
Distance Vector Routing Example-
Consider-
- There is a network consisting of 4 routers.
- The weights are mentioned on the edges.
- Weights could be distances or costs or delays.
Step-01:
Each router prepares its routing table using its local knowledge.
Routing table prepared by each router is shown below-
At Router A-
| Destination | Distance | Next Hop |
| A | 0 | A |
| B | 2 | B |
| C | ∞ | – |
| D | 1 | D |
At Router B-
| Destination | Distance | Next Hop |
| A | 2 | A |
| B | 0 | B |
| C | 3 | C |
| D | 7 | D |
At Router C-
| Destination | Distance | Next Hop |
| A | ∞ | – |
| B | 3 | B |
| C | 0 | C |
| D | 11 | D |
At Router D-
| Destination | Distance | Next Hop |
| A | 1 | A |
| B | 7 | B |
| C | 11 | C |
| D | 0 | D |
Step-02:
- Each router exchanges its distance vector obtained in Step-01 with its neighbors.
- After exchanging the distance vectors, each router prepares a new routing table.
This is shown below-
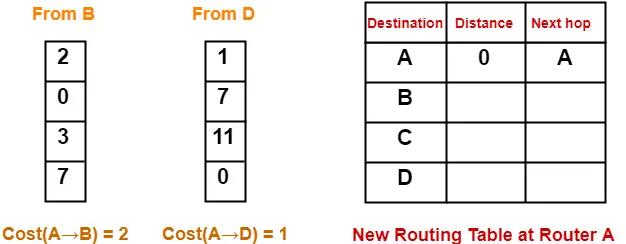
At Router A-
- Router A receives distance vectors from its neighbors B and D.
- Router A prepares a new routing table as-
- Cost of reaching destination B from router A = min { 2+0 , 1+7 } = 2 via B.
- Cost of reaching destination C from router A = min { 2+3 , 1+11 } = 5 via B.
- Cost of reaching destination D from router A = min { 2+7 , 1+0 } = 1 via D.
Explanation For Destination B
- Router A can reach the destination router B via its neighbor B or neighbor D.
- It chooses the path which gives the minimum cost.
- Cost of reaching router B from router A via neighbor B = Cost (A→B) + Cost (B→B)= 2 + 0 = 2
- Cost of reaching router B from router A via neighbor D = Cost (A→D) + Cost (D→B) = 1 + 7 = 8
- Since the cost is minimum via neighbor B, so router A chooses the path via B.
- It creates an entry (2, B) for destination B in its new routing table.
- Similarly, we calculate the shortest path distance to each destination router at every router.
|
Thus, the new routing table at router A is-
| Destination | Distance | Next Hop |
| A | 0 | A |
| B | 2 | B |
| C | 5 | B |
| D | 1 | D |
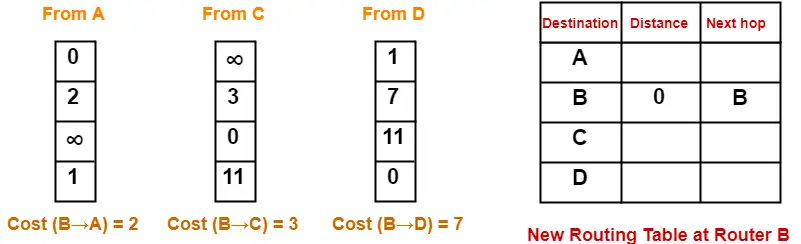
At Router B-
- Router B receives distance vectors from its neighbors A, C and D.
- Router B prepares a new routing table as-
- Cost of reaching destination A from router B = min { 2+0 , 3+∞ , 7+1 } = 2 via A.
- Cost of reaching destination C from router B = min { 2+∞ , 3+0 , 7+11 } = 3 via C.
- Cost of reaching destination D from router B = min { 2+1 , 3+11 , 7+0 } = 3 via A.
Thus, the new routing table at router B is-
| Destination | Distance | Next Hop |
| A | 2 | A |
| B | 0 | B |
| C | 3 | C |
| D | 3 | A |
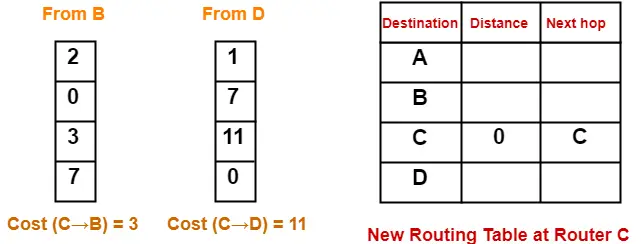
At Router C-
- Router C receives distance vectors from its neighbors B and D.
- Router C prepares a new routing table as-
- Cost of reaching destination A from router C = min { 3+2 , 11+1 } = 5 via B.
- Cost of reaching destination B from router C = min { 3+0 , 11+7 } = 3 via B.
- Cost of reaching destination D from router C = min { 3+7 , 11+0 } = 10 via B.
Thus, the new routing table at router C is-
| Destination | Distance | Next Hop |
| A | 5 | B |
| B | 3 | B |
| C | 0 | C |
| D | 10 | B |
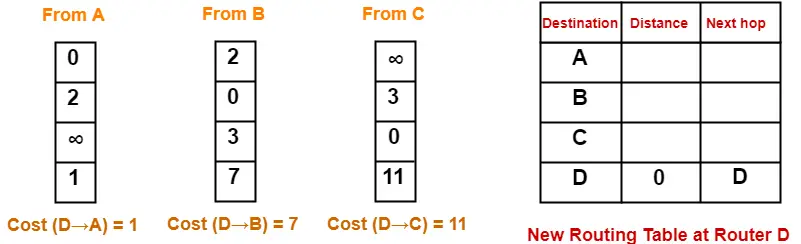
At Router D-
- Router D receives distance vectors from its neighbors A, B and C.
- Router D prepares a new routing table as-
- Cost of reaching destination A from router D = min { 1+0 , 7+2 , 11+∞ } = 1 via A.
- Cost of reaching destination B from router D = min { 1+2 , 7+0 , 11+3 } = 3 via A.
- Cost of reaching destination C from router D = min { 1+∞ , 7+3 , 11+0 } = 10 via B.
Thus, the new routing table at router D is-
| Destination | Distance | Next Hop |
| A | 1 | A |
| B | 3 | A |
| C | 10 | B |
| D | 0 | D |
For final table repeat table one more time itself.
Important Notes-
Note-01:
In Distance Vector Routing,
- Only distance vectors are exchanged.
- “Next hop”values are not exchanged.
- This is because it results in exchanging the large amount of data which consumes more bandwidth.
Note-02:
While preparing a new routing table-
- A router takes into consideration only the distance vectors it has obtained from its neighboring routers.
- It does not take into consideration its old routing table.
Note-03:
The algorithm is called so because-
- It involves exchanging of distance vectors between the routers.
- Distance vector is nothing but an array of distances.
Note-04:
- The algorithm keeps on repeating periodically and never stops.
- This is to update the shortest path in case any link goes down or topology changes.
Note-05:
- Routing tables are prepared total (n-1) times if there are n routers in the given network.
- This is because shortest path between any 2 nodes contains at most n-1 edges if there are n nodes in the graph.
Note-06:
- Distance Vector Routing suffers from count to infinity problem.
- Distance Vector Routing uses UDP at transport layer.
Thank you viewers







Comments
Post a Comment